Blog

Storage in Solidity

By Fran Palacios

In this article, we’re going to delve a bit deeper into persistent storage on EVM-compatible blockchains¹. In other languages, it’s not necessary to know what happens at a low level in order to write efficient code, but in the case of Solidity (which is not quite a high-level language), it is important – though not essential – to know this, because operations cost gas.

Gas is the unit that measures the amount of computational effort required to execute operations on the blockchain. In Ethereum, we have a transactional model, and each transaction requires computation to be executed and validated, so a fee (gas) must be paid. In this table fragment, we can see the cost associated with each operation (opcode); we can see that accesses to Memory (MLOAD & MSTORE) are much cheaper than accesses to Storage (SLOAD & STORE).

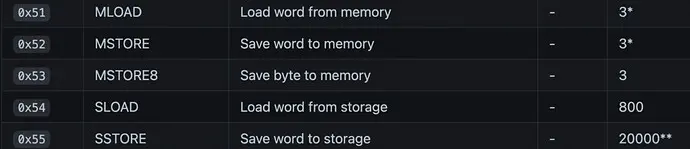
Opcodes table: https://github.com/crytic/evm-opcodes

Memory & Storage

In Solidity, there are two types of storage: volatile (Memory), which can be thought of as RAM, and persistent (Storage), which can be thought of as a hard drive.

Memory: Variables defined in the body of functions (whether or not they contain the memory keyword) are temporary; they only exist within the scope of that function, and they are deleted when the function execution ends until the next execution, where a new storage space is allocated.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


    contract Foo {
    	// State variables
    	uint8[] foo;
    
    	function bar(string memory _bar, bool _foo) public {
            // Memory variables
            uint8 baz = 10;
            // Copy of foo, modifications to _baz doesn't affect the foo state
            uint8[] memory _baz = foo;
        }
    }

Storage: Variables defined outside of functions are considered persistent by default (known as state variables). These variables persist on the blockchain.

1
2
3
4
5
6
7
8
9


    contract Foo {
    	// State variables
    	uint8[] foo;
    
    	function bar() public {
    	    // Reference to foo, modifications to _baz alters the foo state
    	    uint8[] storage _baz = foo;
        }
    }

Storage & SmartContracts

All Smart Contracts running on the EVM have a permanent Storage associated with them, which is part of the blockchain’s global state. This Storage can be seen as a list of key-value pairs ordered by their declaration in the Smart Contract, with each element being 32 bytes in size, and a total size of 2^256. While the Storage is large enough to store anything, it initially costs nothing since it’s all set to 0. In Ethereum, you pay for everything that’s not 0 and for memory expansions.

The order in which variables are declared is relevant in Solidity, and they’re usually not grouped by domain or other criteria, but by size and type for the EVM’s convenience.

Let’s take a look at this contract.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


// SPDX-License-Identifier: MIT
pragma solidity ^0.8.7;

contract StoragePlayground {
  // State  variables
  uint256 favNumber; // Storage at slot 0
  bool someBool;     // Storage at slot 1

  constructor() {
     favNumber = 5;
     someBool = true;
  }
}

To inspect the state of the Storage, we can use the getStorageAt function provided by the provider (in this case, we’ll use ethers). We pass it the address of a contract and the memory slot of the data we want to retrieve. This function allows us to examine the contents of the Storage at a specific slot, which can be useful for debugging and analyzing Smart Contracts on the blockchain.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


// Pseudocode to deploy the smart contract locally
function deployContract() {
  console.log('Deploying StoragePlayground...');
  const contract = await deploy('StoragePlayground', {...});

  for (let slot = 0; slot < 5; slot++) {
    let content = await ethers.provider.getStorageAt(contract.address,slot)
    console.log(`${slot} -> ${content}`)
  }
}

This piece of code prints out to the console the first 5 slots in the contract storage.

1
2
3
4
5


0 -> 0x0000000000000000000000000000000000000000000000000000000000000005
1 -> 0x0000000000000000000000000000000000000000000000000000000000000001
2 -> 0x0000000000000000000000000000000000000000000000000000000000000000
3 -> 0x0000000000000000000000000000000000000000000000000000000000000000
4 -> 0x0000000000000000000000000000000000000000000000000000000000000000

As expected, the number 5 was stored in position 0 and True in position 1.

If we change the data type of favNumber from uint256 to uint8 we can see how they share a memory slot:

1
2
3
4
5


0 -> 0x0000000000000000000000000000000000000000000000000000000000000105
1 -> 0x0000000000000000000000000000000000000000000000000000000000000000
2 -> 0x0000000000000000000000000000000000000000000000000000000000000000
3 -> 0x0000000000000000000000000000000000000000000000000000000000000000
4 -> 0x0000000000000000000000000000000000000000000000000000000000000000

We can see that the size and type of variables must be taken into account. The rules for declaring variables efficiently are defined in the Solidity documentation.

Arrays & Mappings

Now let’s see some examples using arrays (fixed-size and dynamic) and mappings².

Fixed-size arrays are stored in consecutive positions. We can verify this using the same method as before:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


contract StoragePlayground {
  // State variables
  uint256 favNumber; // Storage at slot 0
  bool someBool; // Storage at slot 1
  uint256[3] myArray; // Storage slots 2,3 and 4

  constructor() {
     favNumber = 5;
     someBool = true;

     myArray = [10, 20, 30];
  }
}

We see that the data stored at slots 2, 3 and 4 are the hexadecimal values of 10, 20 and 30 (0x00..a, 0x00...14 and 0x00...1e)

1
2
3
4
5


0 -> 0x0000000000000000000000000000000000000000000000000000000000000005
1 -> 0x0000000000000000000000000000000000000000000000000000000000000001
2 -> 0x000000000000000000000000000000000000000000000000000000000000000a
3 -> 0x0000000000000000000000000000000000000000000000000000000000000014
4 -> 0x000000000000000000000000000000000000000000000000000000000000001e

And what about dynamic arrays? How does the EVM know how many slots to reserve between variables?

Well, it doesn’t know 😅, and to solve this it uses a hash function keccak256, to find a memory position and not overwrite other slots. Let’s change the code a bit to add a dynamic array. Reemplazamos uint256[3] myArray con uint256[] myArray. The rest of the code remains the same with the same 3 elements.

1
2
3
4
5


0 -> 0x0000000000000000000000000000000000000000000000000000000000000005
1 -> 0x0000000000000000000000000000000000000000000000000000000000000001
2 -> 0x0000000000000000000000000000000000000000000000000000000000000003
3 -> 0x0000000000000000000000000000000000000000000000000000000000000000
4 -> 0x0000000000000000000000000000000000000000000000000000000000000000

We can see that they’re gone,but in position 2 we have stored the number 3, which represents the length of the array and gets updated as elements are added. However, the slot where it is stored remains the same, which is slot 2. To calculate the position from which the array data is stored, the function keccak256(slot-where-the-array-length-is-stored) is used. Ethers provides us with this function:

We know that it is in slot 2 (0x2 in hexadecimal). With hexZeroPad, we fill in 0s to the left until we reach 32 bytes (64 zeros).

1
2
3
4


const arrayLengthSlot = ethers.utils.hexZeroPad('0x2', 32);
// 0x0000000000000000000000000000000000000000000000000000000000000002
const firstElementSlot = ethers.utils.keccak256(arrayLengthSlot);
// 0x405787fa12a823e0f2b7631cc41b3ba8828b3321ca811111fa75cd3aa3bb5ace

Now, if we call getStorageAt with that slot, we will get the first item stored in the array:

1
2


let content = await ethers.provider.getStorageAt(contract.address, firstElementSlot)
// 0x000000000000000000000000000000000000000000000000000000000000000a

We see that the hexadecimal value of 10, our first element! Now the next elements are stored in a sequentiall order. So if we add 1 to the position of the first element we get the second.

1
2
3
4
5
6
7


// 0x405787fa12a823e0f2b7631cc41b3ba8828b3321ca811111fa75cd3aa3bb5ace
// + 1
// 0x405787fa12a823e0f2b7631cc41b3ba8828b3321ca811111fa75cd3aa3bb5acf
//                                                                  ^
const secondElementSlot = '0x405787fa12a823e0f2b7631cc41b3ba8828b3321ca811111fa75cd3aa3bb5acf'
content = await ethers.provider.getStorageAt(contract.address, secondElementSlot)
// 0x0000000000000000000000000000000000000000000000000000000000000014

Which is 20 in hex. And the third element is in the next one:

1
2
3
4


// 0x405787fa12a823e0f2b7631cc41b3ba8828b3321ca811111fa75cd3aa3bb5acf
// +1 
// 0x405787fa12a823e0f2b7631cc41b3ba8828b3321ca811111fa75cd3aa3bb5ad0
//                                                                 ^^

Finally, we will see an example with mappings.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


contract StoragePlayground {
  // State variables
  uint256 favNumber; // Storage at slot 0
  bool someBool; // Storage at slot 1
  mapping(uint256 => bool) dictionary; // Storage at slot 2
  address private someAddress; // Storage at slot 3

  constructor() {
    favNumber = 5;
    someBool = true;
    someAddress = 0xaA3052db3062D60643682B1272d00A6BF4A6f5E6;
    dictionary[10] = true;
    dictionary[20] = false;
    dictionary[30] = true;
  }
}

In this output, we see that slot 2 is completely empty, unlike the dynamic array, here the length of the mapping is not stored because it is not iterable, and its keys do not have to be consecutive.

1
2
3
4
5


0 -> 0x0000000000000000000000000000000000000000000000000000000000000005
1 -> 0x0000000000000000000000000000000000000000000000000000000000000001
2 -> 0x0000000000000000000000000000000000000000000000000000000000000000
3 -> 0x000000000000000000000000aa3052db3062d60643682b1272d00a6bf4a6f5e6
4 -> 0x0000000000000000000000000000000000000000000000000000000000000000

However, to calculate the memory position to store the data, it does something similar to arrays. In this case, the formula to apply is this: keccak256(h(k) . p). Where h is a function based on the type of the key, k is the dictionary key, p is the memory slot of the mapping, and . is the concatenation of both.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


// Convert to hexadecimal the slot 0x2 and the dictionary key
const p = ethers.utils.hexZeroPad('0x2', 32);
const keyAsHex = ethers.BigNumber.from(10).toHexString();
const h_k_ = ethers.utils.hexZeroPad(keyAsHex, 32);

// Concat
const concat = ethers.utils.concat([h_k_, p]);

// Apply hash
const concatHash = ethers.utils.keccak256(concat);

// Get the date
const valor = await ethers.provider.getStorageAt(contract.address,concatHash);

// This would be the output of concatHash and the value for the 3 keys
// dictionary[10] = true
// 0xd3604db978f6137b0d18816b77b2ce810487a3af08a922e0b184963be5f3adfc
// 0x0000000000000000000000000000000000000000000000000000000000000001

// dictionary[20] = false
// 0x50d9dffd10eb4437a15e8bb1c50afee98ea231805f136fb9a057e7aaeec448ae
// 0x0000000000000000000000000000000000000000000000000000000000000000

// dictionary[30] = true
// 0x6ea47ca2f9e3a67b0e336c514aa9f125109f49309b7162caec32e7d27e5c838c
// 0x0000000000000000000000000000000000000000000000000000000000000001

getStorageAt

As a curiosity about this function, it allows us to access the contents of a memory slot in a contract’s storage. If you think about it, you can see everything, as long as you have access to the contract, you can see in which slot something is stored.

As seen in the last example, there are public variables (by default) and private ones (those that have the private 3121prefix), so using this function, you can see them all if you have access to the contract code and simply count in which slot the variable is defined. So remember, never store sensitive data in the blockchain.

Recursos

keccak256 playground

hex-to-decimal converter

Solidity documentation

ethers.utils documentation

Supporting repository

Adrian Hetman post

Footnotes

Ethereum Virtual Machine. It is an entity supported by the nodes that make up the network. We can see it as a distributed state machine. It does not share resources in terms of computing power with other nodes, but it does share global state. It is capable of executing code. ↩︎
It is a key-value dictionary, it is not iterable and its size is dynamic. Its syntax is (key-type ⇒ key-value-type) variable-name. Mappings can be nested. ↩︎

Published on 2022/10/19 by

Fran Palacios

Do you want more? We invite you to subscribe to our newsletter to get the most relevan articles.

If you enjoy reading our blog, could you imagine how much fun it would be to work with us? let's do it!

You may hire us to outsource project development
Or perhaps you just need a hand with your current project.
You are also more than welcome to join our team